产品简介

　　设计方法中涉及了很多复杂的理论分析和计算。针对上述缺点，介绍一种使用 EDA 软件进行电路的设计步骤，然后给出了在 Proteus 中对所设计的滤波器进行仿 真分析和测试的方法。测试根据结果得出，使用该方法设计的带通滤波器具有稳定性很高。设计难度小等优点，也为滤波器的设计提供了一个新的思路。

　　带通滤波器是一种仅允许特定频率通过，同时对其余频率的信号进行相对有效抑制的电路。由于它对信号具有选择性， 故而被广泛地应用现在电子设 计中。但是， 带通滤波器的种类非常之多， 各个类型的设计差异也很大， 这就导致了在传统滤波器的设计方法中不可避免地要进行大量的理论计算与分析，不但损失了宝贵的时间， 同时也提升了电路的设计门槛。未解决上述弊端，本文介绍了一种使用FilterPro 和 Proteus 相结合的有源带通滤波器的设计的具体方案，随着EDA 技术的持续不断的发展，这种方法的优势也将越来越明显。

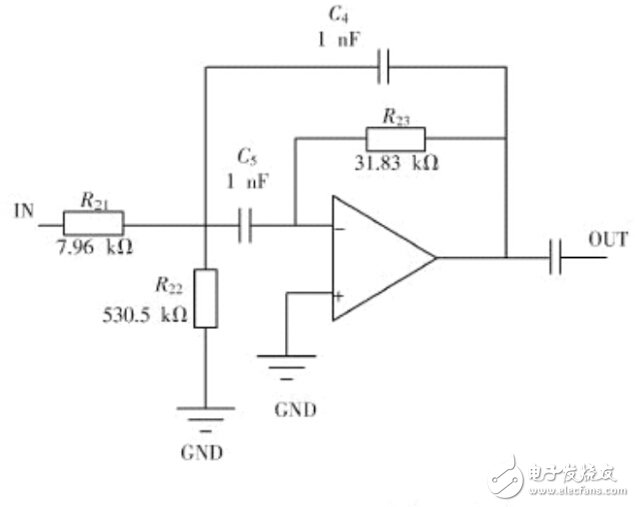
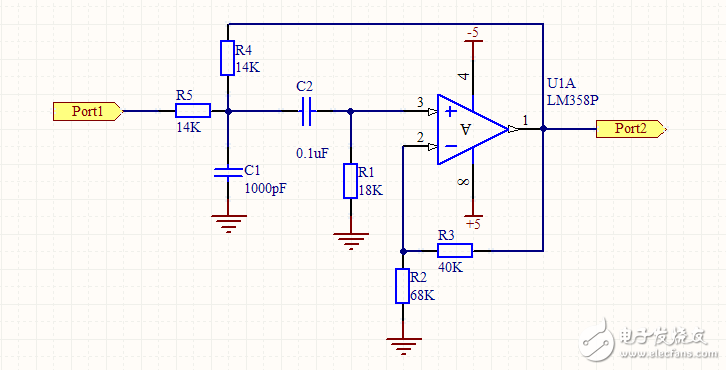
　　电路原理图如图1所示。然后可在 Proteus 中搭建电路进行仿真分析， 前面已经提到， FilterPro 生成的滤波器中的运放使用的理想运放模型，所以仿真时需要先用理想运放做多元化的分析，然后再进行替换。

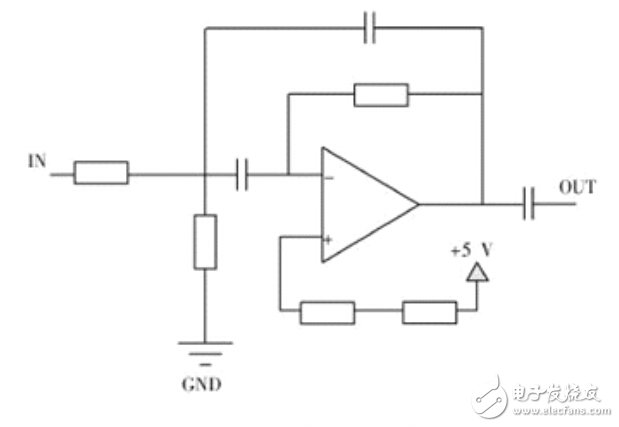
　　设计中运放选择TI产品典型的通用双放LM358，LM358里面包括两个高增益、独立的、内部频率补偿的双运放，适用于电压范围很宽的单电源，而且也适用于双电源工作方式，特点方面具有低输入偏置电流、低输入失调电压和失调电流，它的共模输入电压范围较宽，差模输入电压范围等于电源电压范围，单电源供电电压3-32V，双电源供电1.5-16V，单位增益带宽为1MHz，适用于一般的带通滤波器的设计，同时具有低功耗的功能，对于设计阶数相对高一些的带通滤波器的话，能选用TI的四运放LM324，其性能与LM358大体相同，应用起来节约空间。对于运放的要求此设计不是特别高，只要运放的频率满足低通的截止频率即可，如果精确度要求高的话那么首先运放的供电电压要足够稳定，或者选择精密运放，如TLC274A，否则通用的即可，例如推荐 TI的LM224四运放。

　　巴特沃斯带通滤波器幅频响应在通带中具有最平幅度特性，但是从通带到阻带衰减较慢，如果对于过渡带要求稍高，能增加阶数来实现，否则改选用切比雪夫滤波电路。

　　下面讨论设计两种带通滤波器，其一为二阶低通滤波器和二阶高通滤波器组成的四阶带通滤波器，如下图：

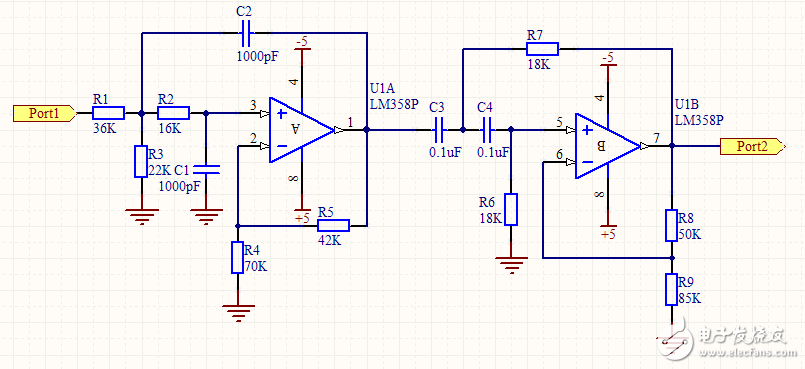
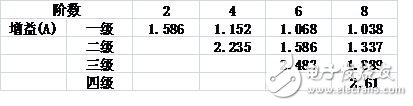
　　对于低通滤波器的设计，电容一般选取1000pF，对于高通滤波器的设计，电容一般选取0.1uF，然后根据公式 R=1/2fc计算得出与电容相组合的电阻值，即得到此图中R2、R6和R7，为了消除运放的失调电流造成的误差，尽量是运放同相输入端与反向输入端对地的直流电阻基本相等，同时巴特沃斯滤波器阶数与增益有一定的关系（见表1），根据这两个条件可以列出两个等式：30=R4*R5/（R4+R5），R5=R4（A- 1），36=R8*R9/（R8+R9），R8=R9（A-1）由此能够解出R4、R5、R8、R9，原则是根据现实情况稍调整电阻值保持在一定限度内即可，不要相差太大，注意频率别超过运放的标定频率。

　　编辑点评：本文介绍的这种带通滤波器的设计方法有着非常强的通用性。实践表明，该方法不仅能避免一些复杂的理论计算和分析，同时通过仿真还可以直观的检验电路的输入和输出，进而时滤波器的性能更的稳定。